728x90
반응형
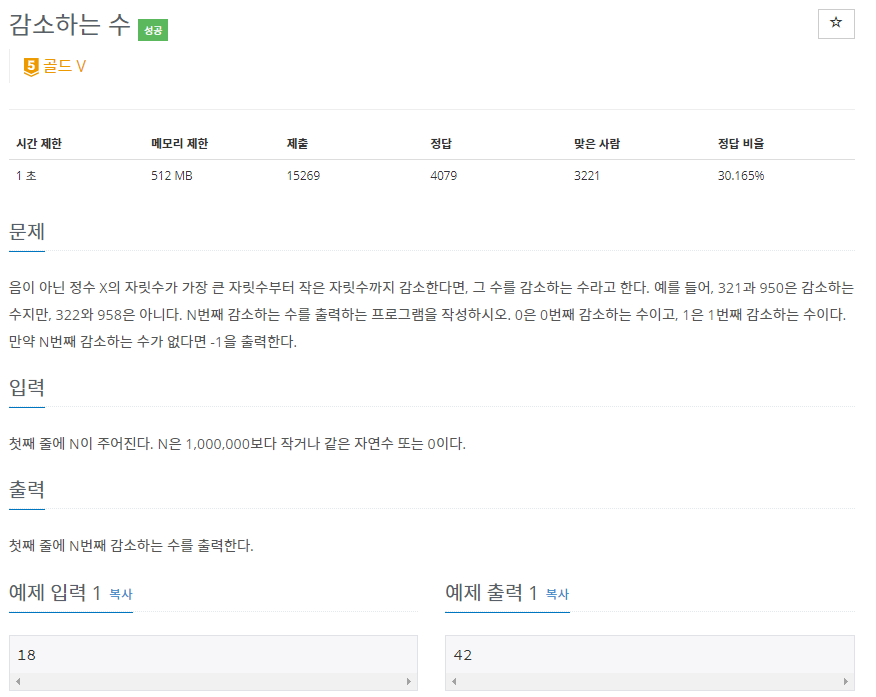
백준 1038 감소하는 수
1. 문제
2. 접근법
[ 문제 접근 ]
1. 우선 감소하는 수를 차례대로 나열 해 보면 아래와 같다.
0 1 2 3 4 5 6 7 8 9 10 20 21 30 31 32 40 41 42 43 50 51 52 53 54 . . .
규칙을 생각 해 보면
1) 감소하는 수는 0 ~ 9까지 몇개의 숫자를 뽑아도 단 하나만 나온다.
2) 십의 자리 숫자는 1부터 하나씩 커진다.
3) 일의 자리 숫자는 해당 수를 10으로 나누었을때의 나머지이고 0보다 크고 십의 자리 숫자보다 항상 작다.
2. 감소하는 수가 없는 경우를 판별하는 기준은 블로그를 찾아봤다.
0~9까지 나올수 있는 감소하는 수는 공집합이 아닌 임의의 부분집합의 수를 구하는 경우와 같다.
따라서, 감소하는 수는 2^10 - 1 = 1023개가 나온다.
3. 코드
#include <algorithm>
#include <iostream>
#include <fstream>
using namespace std;
long long arr[1000001]; //최대 100만번째 수까지 구할 수 있으므로 범위를 longlong형으로 바꿔줌
int main()
{
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int n, tmp = 0;
cin >> n;
//10보다 작은 경우에는 입력받은 수 그대로 출력해주면 됨
if (n < 10)
{
cout << n << "\n";
return 0;
}
//1023개 이상인 경우는 -1출력
else if (n >= 1023)
{
cout << -1 << "\n";
return 0;
}
//10이상 1023 미만인 경우
else if (10 <= n && n < 1023)
{
//arr에 0~9까지 값 넣어줌
for (int i = 0; i < 10; i++)
{
arr[i] = i;
}
//arr 10부터는 입력받은 값까지 돌면서 각 자릿수 구해주면 됨
int num = 10;
for (int i = 1; i <= n; i++)
{
//일의 자릿수(이전 자릿수)
int before = arr[i] % 10;
//다음 자릿수는 이전 자릿수의 범위까지 돌면서 하나씩 더해주면 됨
for (int j = 0; j < before; j++)
{
arr[num++] = (arr[i] * 10 + j);
}
}
cout << arr[n] << "\n";
return 0;
}
}4. 시간복잡도
최대 이중 for문을 돌리므로 계산해보면 1022*10(0~9) = 10220, 따라서 1초내에 구현 가능하다.
5. 결과

728x90
반응형
'알고리즘 스터디' 카테고리의 다른 글
| [백준] 2579 계단 오르기(C++) (0) | 2021.09.07 |
|---|---|
| [프로그래머스] 키패드 누르기(C++) (0) | 2021.09.03 |
| [프로그래머스] 직업군 추천하기 (0) | 2021.08.31 |
| [백준] 17143 낚시왕(C++) (0) | 2021.08.28 |
| [프로그래머스] 오픈채팅방(C++) (0) | 2021.08.27 |


